Créer un dégradé d'image : un vrai défi
Sommaire
Trier des images pour les classer en dégradé de couleur, voilà quelque chose qui paraît trivial et sans intérêt au premier abord, et si c’était en réalité beaucoup plus difficle et intéressant que ça ? Le code en Python est disponible sur mon Github.
Un feed Instagram pas comme les autres #
Le feed est l’ensemble des publications d’un compte Instagram, c’est là où sont regroupées toutes vos photos, vos réels etc… C’est la partie visible du compte, il doit être le plus attirant possible afin de susciter de l’engagement.
Je discutais avec une amie à propos de mon bot Instagram, @archie_the_aesthete, qui ne trouve pas son public (d’ailleurs si vous voulez savoir comment je l’ai créé, je vous invite à lire mon article à ce propos : J’ai créé un bot Instagram 100% légal et totalement automatisé). Selon elle, le principal défaut de mon bot est qu’il n’a pas un beau feed. Pour illustrer l’importance de ce critère, elle me fait découvrir le compte Insta de @charlie__danger, tout en se demandant comment cette créatrice peut faire pour arriver à un tel résultat. Je vous invite d’ailleurs à suivre cette personne sur Youtube si vous aimez l’Archéologie et l’Histoire.

J’émets alors l’hypothèse d’un algorithme qui classerait les images, tout en imaginant les grandes ligne du programme. Je lui indique alors que cela ne me semble pas compliqué au premier abord (quelle erreur à posteriori !) et que je pourrais même le développer pour elle. Je n’imaginais pas tout ce qui se cachait derrière…
Une approche bien trop naïve #
La première étape est d’extraire, pour chaque image, les informations permettant de savoir si elle est plutôt bleue, verte ou jaune. J’ai tout d’abord pensé à extraire la couleur moyenne de chaque image, je suis tombé sur cette question Stackoverflow : How to find the average colour of an image in Python with OpenCV?. Là-bas, un utilisateur visiblement bien plus callé en imagerie que moi conseille plutôt d’utiliser les couleurs dominantes plutôt que la couleur moyenne. Pourquoi ? Car la couleur moyenne ne fait pas resortir les dominantes de couleurs que l’humain voit, or, c’est justement ce que je recherche ici ; créer de la cohérence pour l’oeil humain.
Il explique et illustre le concept de couleur dominante d’une image dont voici une traduction en français (reponse de Tonechas sur le post Stackoverflow, je vous invite à lire sa réponse si le sujet vous intéresse, c’est très bien détaillé) :

Voyons comment se présentent ces couleurs pour mieux comprendre les différences entre les deux approches. Dans la partie gauche de la figure ci-dessous est affichée la couleur moyenne. Il apparaît clairement que la couleur moyenne calculée ne décrit pas correctement le contenu en couleur de l'image originale. En fait, il n'y a pas un seul pixel avec cette couleur dans l'image originale. La partie droite de la figure montre les cinq couleurs les plus représentatives triées de haut en bas par ordre décroissant d'importance (fréquence d'apparition). Cette palette met en évidence que la couleur dominante est le rouge, ce qui est cohérent avec le fait que la plus grande région de couleur uniforme dans l'image originale correspond à la pièce de Lego rouge.

Du calcul de “K-means clustering” #
Théorie #
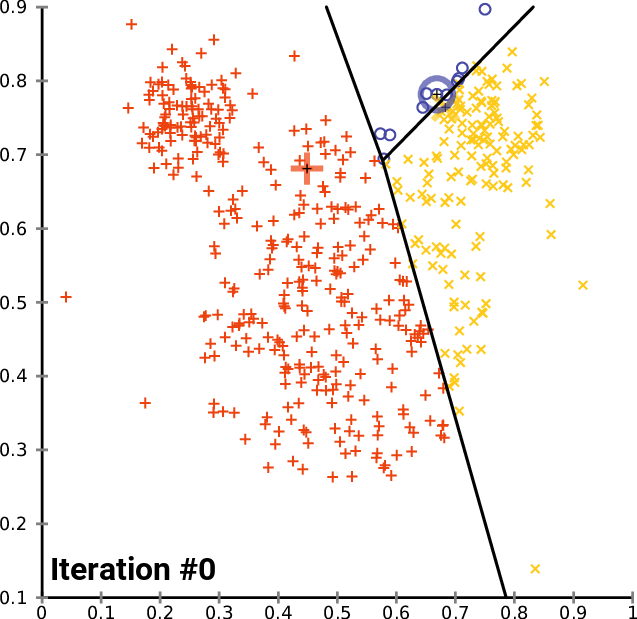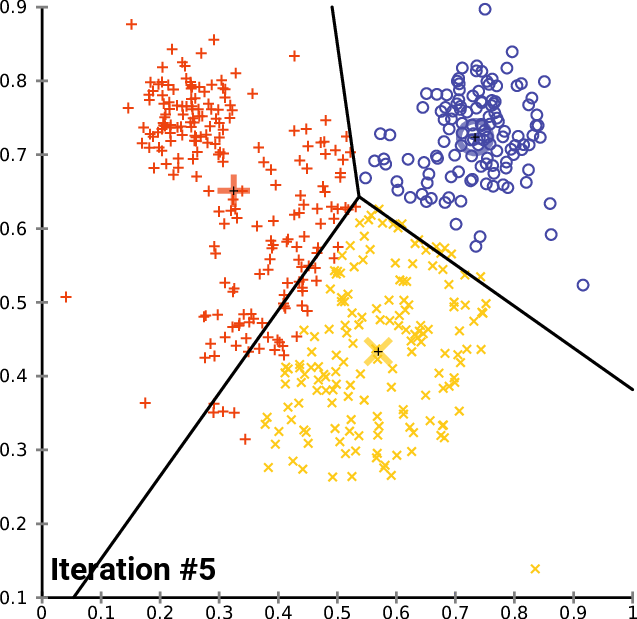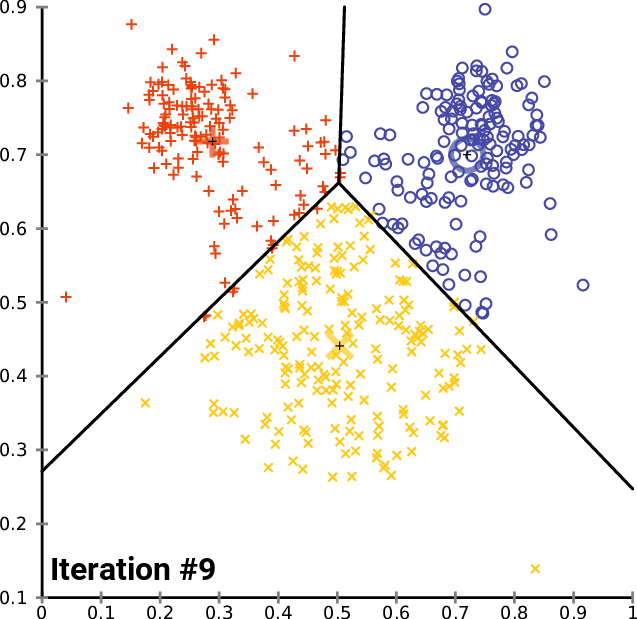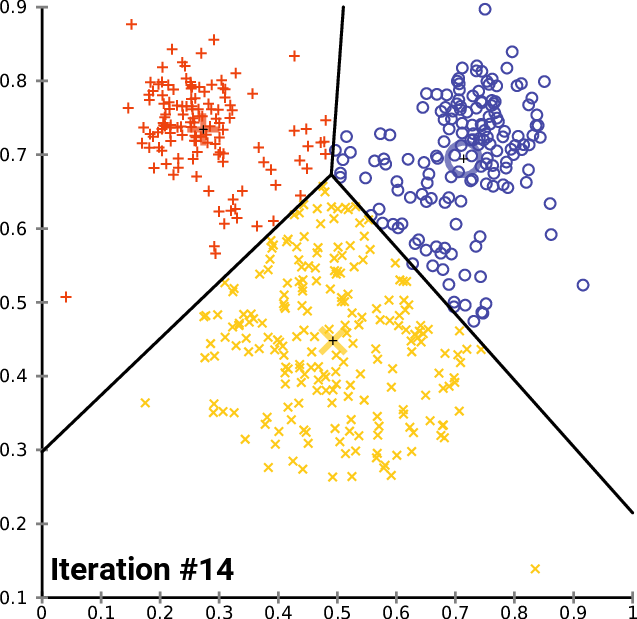
Une méthode pour calculer les couleurs dominantes est le K-means clustering, ou K-moyennes en français. Je ne vais pas rentrer dans les détails de cette méthode, déjà car je ne suis pas compétent, mais également car ça n’est pas le sujet de l’article. Je vous invite à consulter cette page : Wikipédia - k-means clustering si le sujet vous intéresse (la page en anglais est plus complète que celle en français). Car une illustration vaut plus que mille mots, ce gif devrait vous aider à sentir ce que permet de faire le k-mean-clustering.
Cette animation ci-dessous montre qu’au fur et à mesure des itérations, nos 3 points noirs se rapprochent de ce qui semble être 3 points moyens de nos 3 sous-ensembles (rouge, jaune et bleu), on appelle ça les centres de cluster, ou centroïdes de cluster. C’est ce qu’on appelle la convergence des k-moyennes. Ici, on a définit arbitrairement qu’il nous fallait découper tous nos points en 3 sous-ensemble, ça aurait pu être 4, 2, 37… On a aussi définit arbitrairement qu’il fallait itérer (faire le calcul) 14 fois, plus on met d’itération et plus on se rapproche de la véritable moyenne (mais plus les calculs sont longs). L’idée étant de tendre vers k points (ici 3) qui sont au plus proches de tous les autres points du sous-ensemble. Ce faisant, on partitionne nos données en k-ensemble.
Pratique avec exemples #
J’ai choisi de régler mon calcul des k-moyennes de sorte à trouver les 5 couleurs dominantes en 300 itérations (valeur par défaut). Peut-être que ces paramètres ne sont pas optimaux en terme de performance (on verra plus bas que ce sont ces calculs qui ralentissent mon programme), mais pour le moment ils me suffisent à produire un résultat satisfaisant.
Voici plusieurs exemples pour se convaincre que cette méthode produit des résultats intéressants, sous chaque image vous avez les 5 couleurs dominantes produites à partir de la méthodes des k-means clustering, plus la couleur est dominante, plus le rectangle associé est grand :

Le tri : encore une approche naïve #
Maintenant que je suis parvenu à isoler les couleurs dominantes de mes images, il faut les classer pour obtenir un dégradé de couleur. J’ai donc créé une structure de donnée qui se présente comme suit :
{
'image1.jpg': [
[pourcentage_couleur1, R, G, B],
[pourcentage_couleur2, R, G, B],
[pourcentage_couleur3, R, G, B],
[pourcentage_couleur4, R, G, B],
[pourcentage_couleur5, R, G, B]
],
'image2.png':[
[pourcentage_couleur1, R, G, B],
[pourcentage_couleur2, R, G, B],
[pourcentage_couleur3, R, G, B],
[pourcentage_couleur4, R, G, B],
[pourcentage_couleur5, R, G, B]
],
...
}Chaque image est indexée par son nom et comporte ses données associées. Il reste ensuite à les classer. Ma première apprcoche fut la suivante :
- prendre la première couleur dominante de ma première image dans ma structure
- parcourir toutes les autres images et trouver celle qui a la couleur dominante la plus proche de mon image courante
- sauvegarder cette seconde image comme étant la plus proche de ma première
- supprimer cette image de ma structure de donnée
- recommencer jusqu’à ce qu’il n’y ait plus d’image dans ma structure de donnée
Vous avez dit une couleur proche ? #
parcourir toutes les autres images et trouver celle qui a la couleur dominante la plus proche de mon image courante
Comment faire ça ? Une approche intuitive serait de calculer la distance entre 2 couleurs. Une couleur peut être représentée par 3 entiers : sa composante rouge, verte et bleue, allant de 0 à 255. C’est ce qu’on appelle le RGB. On peut donc représenter une couleur comme étant un point dans un espace en 3 dimensions. Un bleu foncé aura cette représentation RGB :
red: 0, green: 18:, blue: 101ce qui donne cette couleur :
Puisqu’une couleur est un point, on peut calculer une distance entre deux points. Pour cela rien de plus simple ; soient deux couleurs c1 et c2 avec pour coordonnées respectivement rc1, gc1, bc1 et rc2, gc2, bc2, alors la distance entre ces deux couleurs se calcule comme étant :
distance = (r, g, b)
distance = (rc2-rc1, gc2-gc1, bc2-bc1)Une distance étant toujours positive, je fais passer mes trois composantes dans la fonction valeur absolue. Pour rappel : valeur_absolue(-3) = 3 et valeur_absolue(5) = 5. Je fais cela pour toutes mes images et je sélectionne l’image qui a la distance la plus courte par rapport à l’image que je souhaite classer.
J’ai vite observé que cette méthode de calcul de distance ne fonctionnait pas. Le défaut est qu’on ne s’intéresse qu’à la couleur la plus dominante. Si on calcule la moyenne pondérée (rappelez-vous, on dispose également du pourcentage de chaque couleur dominante) des 5 couleurs dominantes de l’image et qu’on calcule ensuite la distance, l’algorithme sort un tris intéressant :
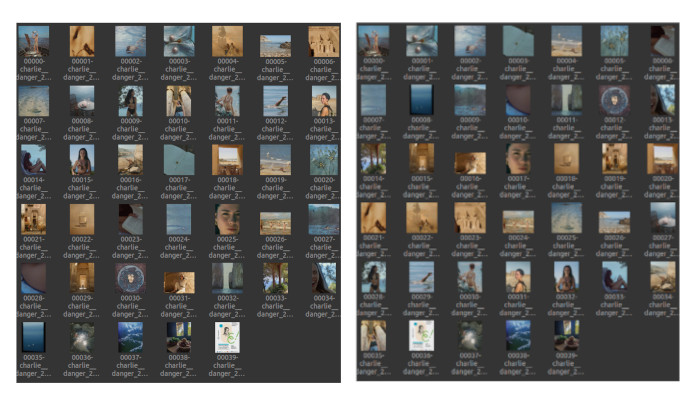
Le tris : pas si simple qu’il n’y paraît #
Le résultat commence à prendre forme mais il y a encore un problème : plus on approche de la fin et moins les images semblent triées. Cela est dû au fait que plus on approche de la fin : plus le choix restant dans les images est limité. Rappelez-vous : on supprime au fur et à mesure les images triées de notre structure de donnée. Pour autant, on ne peut pas laisser les images triées dans notre structure, on tournerait en rond…
Second problème, les images ne sont pas vraiment regroupées par couleurs. Ou plutôt, elles ne sont pas regroupées totalement par couleur. On l’observe déjà sur la partie droite de l’image précédente : on commence par les bleues, suivent les jaunes, puis de nouveau quelques bleues.
Troisième problème, et pas des moindres, ce que j’appelle des divergences locales. Pour illustrer cette idée : regardons le tris produit ci-dessous sur une population plus importante d’images.
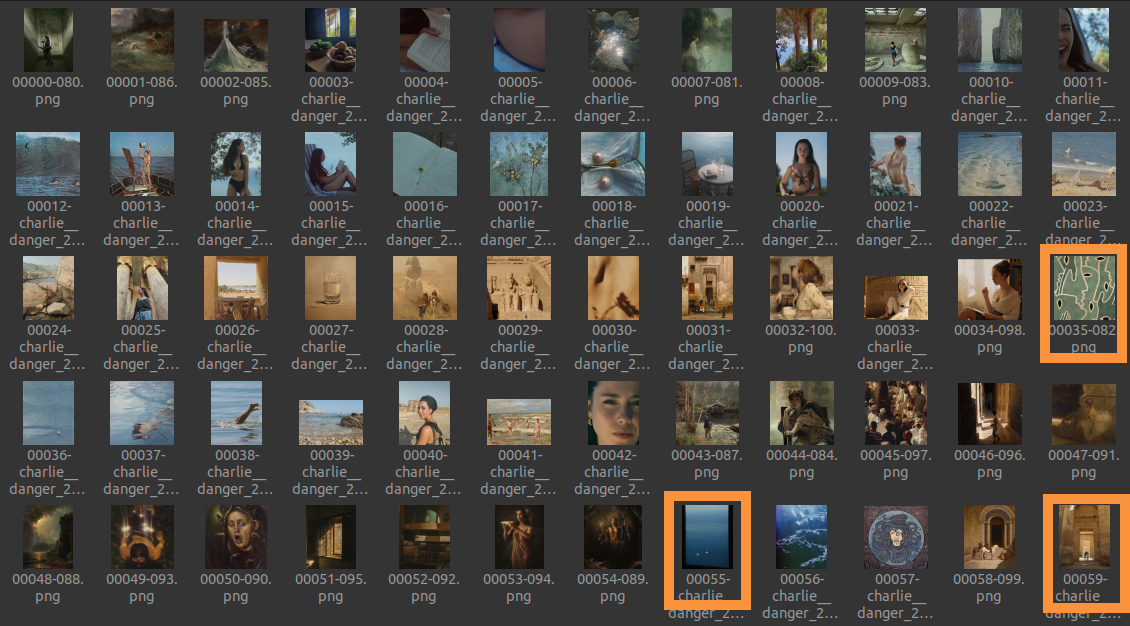
On observe quelques incohérences, j’en ai encadré certaines. Mon hypothèse est que cela est dû à une divergence du tris, je m’explique. Posons six images : A, B, C, D, E et F. Posons que A, B, C et D soient globalement vertes-bleues, et E bleue-jaune (elle apparaîtra donc verte puisqu’on va faire une moyenne) et F jaune. On peut supposer que notre algorithme fasse ce tris :

A ce moment, on observe bien une divergence à partir de C en direction du vert puis du jaune, avant de retourner au bleu plus foncé qui avait été ignoré. A noter que ce problème est différent que le premier énoncé. En effet, il peut rester suffisement d’images après D et une divergence pourra quand même se produire, c’est ce qu’on observe sur l’image avec les encadrés oranges. Cela produira nécessairement une rupture dans notre dégradé alors qu’une meilleure solution est possible.
Un problème sans solution #
Alors je me suis creusé la tête pendant longtemps pour trouver une solution à ce problème. Plus je creusais et plus cela me semblait difficile… J’ai tenté une approche par les graphes, une sorte de plus court chemin et je suis arrivé à la conclusion qu’il me fallait un ordre total entre toutes les couleurs de mes images. Cela me permettrait d’avoir le meilleur tris possible. Pour ceux qui désirent savoir ce qu’est un ordre total, je vous invite à lire cette page : Wikipédia - Ordre total.
Je suis alors tombé sur cet article véritablement passionnant qui répondait en partie à mon problème : The incredibly challenging task of sorting colours. Surprise, il est question d’ordre total ! J’étais sur la bonne voie… Mes espoirs ont cependant été vites douchés lorsque j’ai lu ces lignes :
Supposons que vous représentiez des couleurs avec leurs valeurs RVB, il n'existe pas de moyen standard d'ordonner les triplets dans une ligne, puisqu'ils ne sont naturellement pas organisés de manière linéaire. [...] Je peux vous arrêter ici et vous dire qu'il n'y a pas de solution à ce problème.
Bon, à priori ma recherche était vaine mais la suite de l’article détaille le problème et propose des solutions. Je vous invite à le lire mais la solution que j’ai retenue est celle des plus proches voisins.
Nos chers voisins… #
Parce qu’il n’y avait pas encore assez de pages wikipédia ici, je vais en rajouter une (la dernière), celle à propos de l’algorithme des plus proches voisins : Wikipédia - Nearest neighbour algorithm. Sans rentrer dans le détail, cet algorithme permet de trouver un chemin “optimal” entre des points (cf l’illustration ci-dessous). Nos points sont simplement des valeurs de couleurs, et cet algorithme permet de les trier !
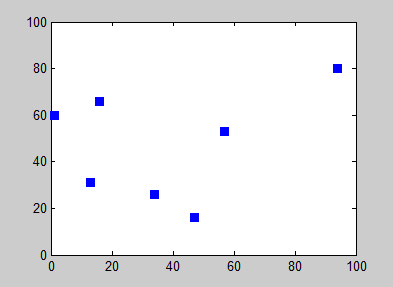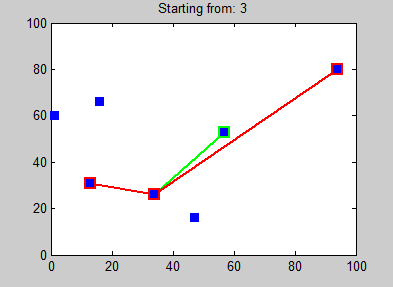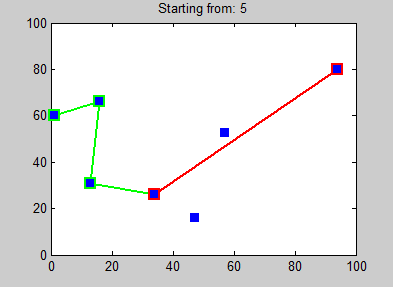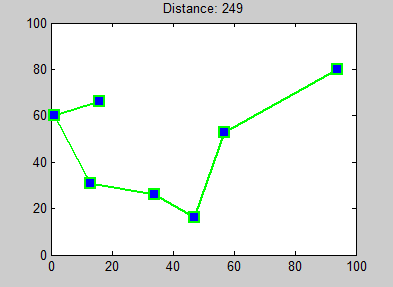
Dernier inconvénient, la complexité de l’algorithme : O(n²). Cela signifie, en gros, que pour n images à trier, on va avoir besoin de n² opérations :
- 10 images : 10² = 100 opérations
- 60 images (environ le nombre que j’avais pour tester mon algorithme) : 3600 opérations
L’implémentation que j’ai trouvée de cet algorithme est optimisée mais on reste dans les mêmes ordres de grandeur. Les résultats obtenus sont sans appels, à gauche, l’ancien algorithme de tris, à droite, le résultat avec l’algorithme des plus proches voisins :
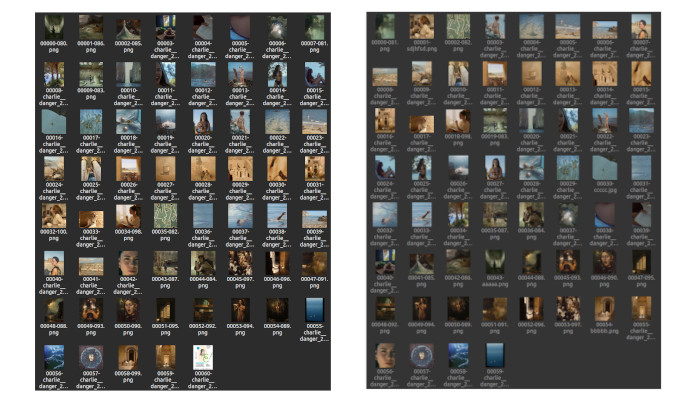
Certes, il existe encore des imperfections (au début), l’algorithme n’est pas parfait mais peut-être est-ce à cause de ma moyenne pondérée. J’ai tenté d’autres approches mais aucune n’a donné un résultat aussi propre que celle-là. On observe que les divergences locales ont disparues ! C’est une réussite sur ce point là !
Optimisations #
Le programme total est assez lent sur mon ordinateur, pour les images ci-dessus, comptez plusieurs minutes. La partie la plus longue est assurément le calcul de clustering ; pour une image de 600 * 800 px il me faut environ 50 secondes pour ce calcul. Est-il possible d’aller plus vite ? Oui, et pour cela il faut faire des tests.
Retour sur le clustering #
On l’a vu, le clustering consiste à répéter des calculs pour aboutir à plusieurs valeurs. En creusant un peu, on s’apperçoit que la librairie utilisée fait par défaut 300 itérations. Que se passe-t-il si on diminue ? Surtout, est-ce que nos valeurs de couleurs dominantes sont encore précises ?
| nombre itérations | temps de calcul (s) | pourcentage de temps économisé (%) | résultat du clustering |
|---|---|---|---|
| 300 | 57 | - | [[36, 37, 28, 22], [26, 140, 99, 43], [24, 96, 62, 25], [7, 0, 0, 0], [4, 200, 164, 115]] |
| 150 | 52 | 9 | [[36, 37, 28, 22], [26, 140, 99, 43], [24, 96, 62, 25], [7, 0, 0, 0], [4, 199, 163, 114]] |
| 50 | 37 | 35 | [[36, 37, 28, 22], [27, 139, 98, 42], [24, 96, 62, 25], [7, 0, 0, 0], [4, 199, 163, 114]] |
| 10 | 31 | 46 | [[36, 37, 28, 22], [26, 140, 99, 43], [24, 96, 62, 25], [7, 0, 0, 0], [4, 200, 163, 114]] |
| 2 | 25 | 56 | [[36, 38, 29, 22], [26, 139, 99, 42], [24, 98, 64, 25], [7, 0, 0, 0], [5, 196, 159, 110]] |
On voit ici qu’on peut descendre jusqu’à 2 itérations sans que nos résultats de calculs soient impactés de façon significatives, on a déjà gagné 56% de temps de calcul environ. Pour garder de la marge, j’ai choisis d’effectuer 5 itérations.
time. C’est une méthode de mesure largement imparfaite lorsqu’on veut être précis ou mesurer de petites différences. L’idée ici est de “sentir” les ordres de grandeur.On peut également diminuer le nombre de cluster (couleur dominante) à calculer. Cependant, diminuser le nombre de couleurs dominantes c’est perdre en précision pour des impacts sur la performance qui sont minimes. Pour 4 clusters et 5 itérations on est à 25 secondes, 3 clusters et 5 itérations : 23 secondes et enfin 2 clusters et 5 itérations : 10 secondes. Perdre ne serait-ce qu’une couleur va impacter la pertinence du tris, ça n’est pas acceptable.
Une troisième idée est celle de réduire la taille des images seulement pour le calcul. Juste avant le calcul du clustering, on redimensionne l’image ce qui engendre une forte réduction du volume de donnée à calculer. En effet, pour une image deux fois plus petite on divise par 4 son nombre de pixels. La question reste toujours la même, jusqu’à quand peut-on réduire la taille d’une image sans que cela n’impacte trop la pertinence du tris ? J’ai fais quelques tests et la solution qui me semble être optimale dans mon cas est de fixer une taille maximale à mon image. En effet, si on divise systématiquement la taille de l’image par deux avant le clustering, notre programme ne sera pas adapté à de petites et à des très grandes images. Pour les premières il n’y aura plus assez de pixels et pour les secondes il y en aura encore bien trop.
En fixant une largeur maximale de 2000 pixels (la hauteur est calculée pour garder les proportions de l’image), j’observe que mes résultats ne bougent que très peu pour un gain important. Pour une image de 1.6Mo, avec les optimisations évoquées ci-dessus, on arrive à presque 85% de temps de calcul en moins.
Enfin, on pourrait créer un fichier JSON qui contiendrait les valeurs de clustering pour chaque hash d’image. Puisqu’un hash est unique, il suffirait de hasher l’image, regarder si ce hash se trouve dans le fichier, et si c’est le cas utiliser les valeurs déjà calculées précédemment. Le gain dépend de la façon dont on utilise le programme. En effet, si on veut par exemple construire un beau dégradé, on va souvent traiter les mêmes images en ajoutant quelques nouvelles ; inutile de calculer ce qui a déjà était fait auparavant.
Conclusion #
Il est fascinant de découvrir tout ce qui se cache derrière une simple idée : trier des images par couleur. A partir de cette simple demande, j’ai découvert énormément de choses passionnantes. Il est intéressant de constater que plusieurs des techniques évoquées (clustering, proches voisins) sont utilisées dans d’autres pans de l’informatique, comme la Data Science ou l’Intelligence Artificielle. Il y aurait encore tant à dire et à explorer, je n’ai bien entendu pas pu tout mettre ici mais je vous invite vivement à lire les articles mentionnés ici.
J’espère que vous aurez pris plaisir à me lire, autant, je l’espère, que j’en ai pris à découvrir et partager ces savoirs.