↓Aller au contenu
  1. Mes articles/

RSA Ou Comment Vos Cours De 4eme Vous Permettent De Proteger Vos Codes Bancaires

·9 mins
Sommaire

Ce titre n’est (presque) pas une blague. VOUS avez le niveau pour comprendre comment vos données en ligne sont protégées. Oui, même si vous n’avez peut-être pas un bac scientifique, ni même le brevet, je vous assure que si vous vous laissez porter par ces quelques lignes, vous comprendrez tout de l’algorithme de chiffrement RSA. Ce protocole de chiffrement, ou algorithme, tire son nom de ces trois inventeurs, Rivest Shamir et Adleman.

Mise en situation : vous êtes sur Internet en train de choisir votre prochain smartphone, vous l’avez trouvé et vient le douloureux moment du passage en caisse. Vous rentrez vos codes bancaires et ça y est, ce smartphone est à vous. Pendant ce temps là, je suis confortablement installé derrière mon ordinateur et j’espionne vos activités en ligne (tel un « hacker » des films américains, voyez ?), je récupère toutes les données que vous envoyez sur le web. Croyez-moi, cela est d’une simplicité déconcertante. Comment, à ce moment-là, garantir que je ne puisse pas utiliser vos codes bancaires pour vider votre compte en banque ?

In maths we trust #

La réponse est simple : en les rendant illisibles. C’est ce qu’on appelle la cryptographie : transformer un texte qui a du sens en un autre qui n’en a apparemment pas. Cela est utilisé depuis la nuit des temps, Nabuchodonosor (le roi de Babylone), César et d’autres ont utilisé la cryptographie. A l’époque les codes étaient rudimentaires et simples, aujourd’hui cela s’est un peu complexifié. On utilise des protocoles, des modes d’emplois, des chiffrements très puissants. L’un des plus connus et abordables est RSA.

Aujourd’hui, la cryptographie est partout, mais derrière ce nom quasi mystique se cache des mathématiques à la fois très simples et terriblement puissantes. Avant de vous expliquer en quoi consiste RSA, il convient de revoir quelques bases de mathématiques.

En maths il existe pleins de nombre, je ne vous apprends rien. Certains ont des propriétés particulières, c’est le cas de 2,3,5,7,11,13… ce sont des nombres premiers. Ils ont quelque chose de spécial… ils n’ont aucun diviseurs, exceptés 1 et eux-même. Par exemple, si on veut diviser 13 par autre chose que 1 ou 13, on ne trouvera jamais un entier, c’est-à-dire un chiffre sans virgule. Essayez, vous verrez : 13/2=6,5 13/3=4,3, il n’existe aucun nombre excepté 1 ou 13 qui divise 13, ou un nombre premier en général.

Les nombres premiers ont quelques particularités intéressantes. Déjà, il en existe une infinité, c’est prouvé. Se baser sur de l’infini pour faire de la sécurité, c’est terriblement rassurant. Par contre on sait aussi qu’ils se raréfient au fur et à mesure qu’on en cherche des grands, c’est un peu moins pratique. Mais la propriété qui nous intéresse le plus, c’est la décomposition en facteurs premiers d’un nombre…

Prenons un nombre quelconque, par exemple 42. On peut réécrire 42 comme étant 2x3x7. 2, 3 et 7 sont des nombres premiers. On vient donc de décomposer un nombre en le produit de ses facteurs premiers. La propriété qui est intéressante ici, c’est le fait que cette décomposition est unique, c’est un peu comme un identifiant unique pour tout nombre.

Je récapitule, on a d’un côté un identifiant unique, et de l’autre des éléments aux propriétés particulières qui sont en nombre infinis, croyez moi on se rapproche d’un algorithme de chiffrement… il ne manque qu’une dernière chose, de la complexité.

## La complexité

En informatique, quand on parle de complexité, ça ne veut pas dire exactement la même chose que dans le langage courant. La complexité d’un programme informatique, d’un algorithme, peut se comprendre comme étant la mesure d’à quel point la tâche est fastidieuse à réaliser. Par exemple, si je vous demande de retrouver, dans une liste de 100 nombres aléatoires le chiffre 5, la tâche est plus fastidieuse que si la liste de nombre est ordonnée, par exemple dans l’ordre croissant. Dans le second cas, votre recherche sera bien plus rapide. C’est ce qu’on nomme la complexité algorithmique. Plus la complexité d’un algorithme est élevée, et plus l’ordinateur mettra de temps à réaliser la tâche qu’on lui a attribuée. Ni vous ni moi n’aimons qu’un ordinateur « rame » et c’est pourquoi on s’efforce de construire des algorithmes performants. Seulement, en sécurité, on souhaite tout l’inverse, que certains programmes soient les plus lents possibles. C’est exactement ce qui est recherché en cryptographie. Courage ! Encore quelques lignes et vous allez comprendre …

Revenons à nos nombres. Tout à l’heure nous avons pris un nombre au hasard, 42, et nous l’avons décomposé en le produit de ses facteurs premiers. La tâche n’est pas bien difficile, et par tâtonnement, elle n’a pas pris beaucoup de temps. Cependant, imaginez maintenant que je vous demande la même chose… avec ce nombre :

1 388 657 789

La tâche est autrement plus compliquée, vous ne trouvez pas ? Par contre, vérifier qu’un produit de facteurs premier correspond bien à ce nombre est autrement plus facile ; il suffit de calculer et de comparer. Et bien l’algorithme RSA repose exactement sur ce problème-là.

En d’autre termes, il repose sur le fait qu’un nombre suffisamment grand est très difficilement décomposable en produit de facteurs premiers. Alors même que vérifier si un nombre est bien le résultat d’un produit est simple, l’inverse, c’est-à-dire le décomposer, est autrement plus compliqué. Entendons-nous bien, quand je dis compliqué cela signifie que trouver la décomposition en facteurs premiers est long, même pour un ordinateur. Cela ne signifie pas que c’est “mathématiquement” très compliqué au sens strict du terme, avec beaucoup de temps et de volonté, il serait tout à fait possible d’y arriver. C’est juste très long, et ça l’est aussi pour un ordinateur.

Pour vous donner une image, c’est un peu comme faire un puzzle. Il est très facile, rapide, de vérifier qu’un puzzle est correct, par contre résoudre le puzzle demande beaucoup plus de temps ; c’est un problème asymétrique. Le problème est simple à vérifier mais difficile à résoudre. C’est l’essence même de RSA.

C’est cette asymétrie là qui permet que je ne puisse pas déchiffrer vos codes bancaires chiffrés lorsque vous effectuez un achat en ligne. Avec un nombre de départ, qu’on appelle une clef publique, suffisamment grande, de l’ordre d’un nombre composé de plus de 300 chiffres (oui vous avez bien lu!), il est impossible, dans un temps raisonnable, de trouver sa décomposition en facteurs premiers. Cette décomposition là on l’appelle clef privée, et c’est elle et elle seule qui permet de déchiffrer le message.

Si vous pensez avoir saisi le concept, vous pouvez vous arrêter là. La suite de l’article détaille un exemple de chiffrement avec RSA, c’est un peu plus velu. La partie suivante sert à être plus exhaustif sur le fonctionnement de l’algorithme.

Faisons un exemple #

Construisons une clef publique. Pour cela, rien de plus simple, prenons deux nombres premiers un peu grands, 47 591 et 29 179. Multiplions-les entre-eux et on obtient notre clef publique : 1 388 657 789, cette clef publique permet, avec une fonction mathématique un peu compliquée, de chiffrer un message, par exemple « coucou » en « j@45hqm!îjdf@kd74 ». J’insiste, la clef publique ne sert qu’à chiffrer le message. Cette clef publique n’est un secret pour personne : elle est publique. Même une personne mal intentionnée peut disposer de votre clef publique, ce n’est pas très grave.

Le destinataire de ce message quant à lui dispose de sa clef privée, qu’il ne doit absolument pas dévoiler : ce sont les deux nombres premiers de départ, 47 591 et 29 179, qui est donc la décomposition en facteurs premiers de ma clef publique, et qui permet de déchiffrer le message cryptée, par exemple « j@45hqm!îjdf@kd74 » en « coucou ».

On retrouve bien le message d’origine, et pendant ce temps-là, personne n’a pu découvrir ce qu’il contenait. Pourquoi ça ? Parce qu’il est difficile de retrouver ma clef privée seulement à partir de la clef publique : il est difficile de décomposer 1 388 657 789 comme étant 47 591×29 179, cela est complexe algorithmiquement (souvenez-vous, on a parlé de la complexité plus haut). Or, seule la clef privée permet de déchiffrer « j@45hqm!îjdf@kd74 » en « coucou ».

Voici un schéma qui récapitule ce que je viens d’expliquer.

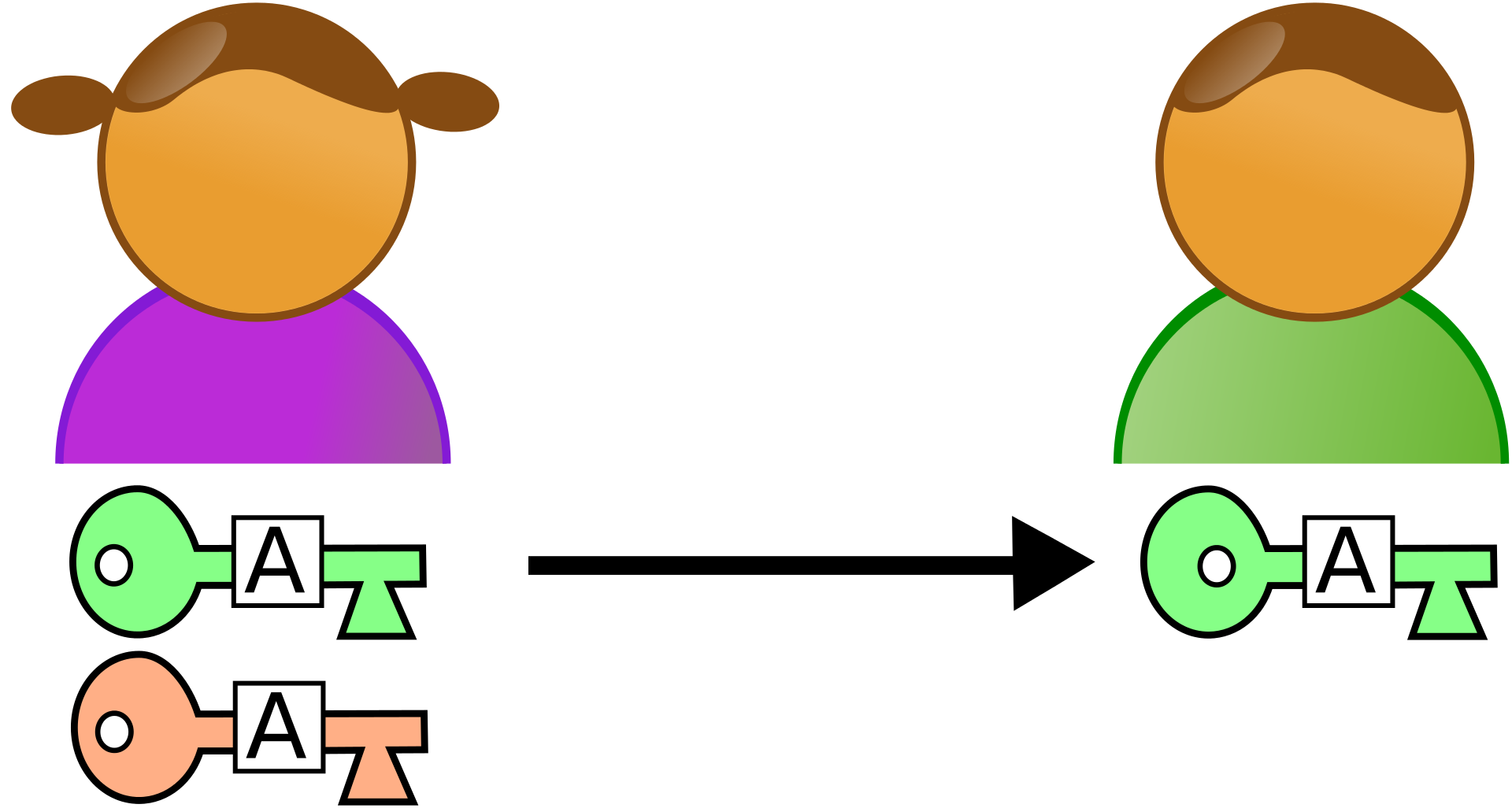
schema 1

Figure 1 : 1re étape : Alice génère deux clefs. La clef publique (verte) qu’elle envoie à Bob et la clef privée (rouge) qu’elle conserve précieusement sans la divulguer à quiconque.

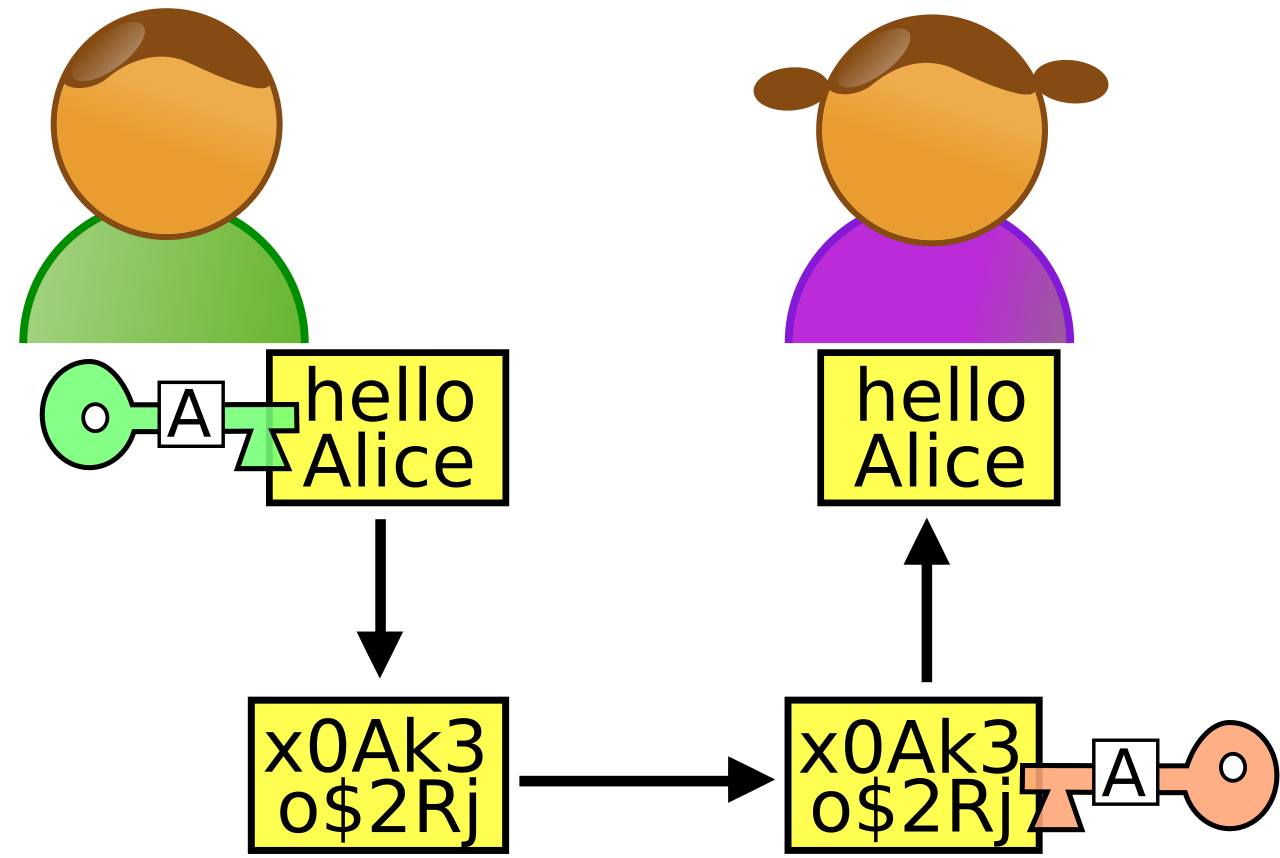
schema 2

Figure 2 : 2e et 3e étapes : Bob chiffre le message avec la clef publique d’Alice et envoie le texte chiffré. Alice déchiffre le message grâce à sa clef privée.

RSA #

Vous savez maintenant comment fonctionne RSA, l’un des protocoles de chiffrement les plus utilisés et connus au monde, qui ne repose sur rien d’autre qu’un problème mathématique rudimentaire. Alors rassurez-vous, présenté comme cela, ce protocole peut vous paraître faible et facilement contournable, mais il n’en est rien. La preuve en est qu’il tient en échec tous ceux qui ont voulu s’attaquer à lui depuis les années 70, et ils sont nombreux.

Françaises, Français, soyez fiers de vos couleurs puisque c’est une équipe de recherche française qui détient le record de performance pour avoir essayé de casser RSA. Sans rentrer dans les détails, ils sont arrivés, en 2012, à factoriser un nombre composé de 250 chiffres dans un temps raisonnable.

Pour aller plus loin #

Sources #

↑